网络流:最大流
EK
增广路方法是很多网络流算法的基础。其思路是每次找出一条从源到汇的能够增加流的路径,调整流值和残留网络 ,直到没有增广路为止。
EK 算法就是不断的找最短路,找的方法就是每次找一条边数最少的增广(即最短路径增广)。
最多要增广多少次?
可以证明,最多 O(VE) 次增广,可以达到最大流。
如何找到一条增广路?
先明确什么是增广路。增广路是一条从s到t的路径,路径上每条边残留容量都为正。把残留容量为正的边设为可行的边,那么我们就可以用简单的 BFS 得到边数最少的增广路。
如何增广?
BFS 得到增广路之后,这条增广路能够增广的流值,是路径上最小残留容量边决定的。把这个最小残留容量 MinCap 值加到最大流值 Flow 上,同时路径上每条边的残留容量值减去 MinCap;最后,路径上每条边的反向边残留容量值要加上 MinCap。这样每次增广的复杂度为 O(E),总复杂度就是 O(VE2)。事实上,大多数网络的增广次数很少,因此 EK 算法能处理绝大多数问题。
为什么增广路径上每条边的反向边残留容量值要加上 MinCap?
残留网络 = 容量网络 - 流量网络
容量网络不改变的情况下,由于增广好比给增广路上通了一条流,路径上所有边流量加 MinCap 之后,相对应的残留网络就发生相反的改变。因为建立了反向边,如果这条路径不是最理想的就会回流,避免了这种情况。这是网络流里很重要的一点。
图例
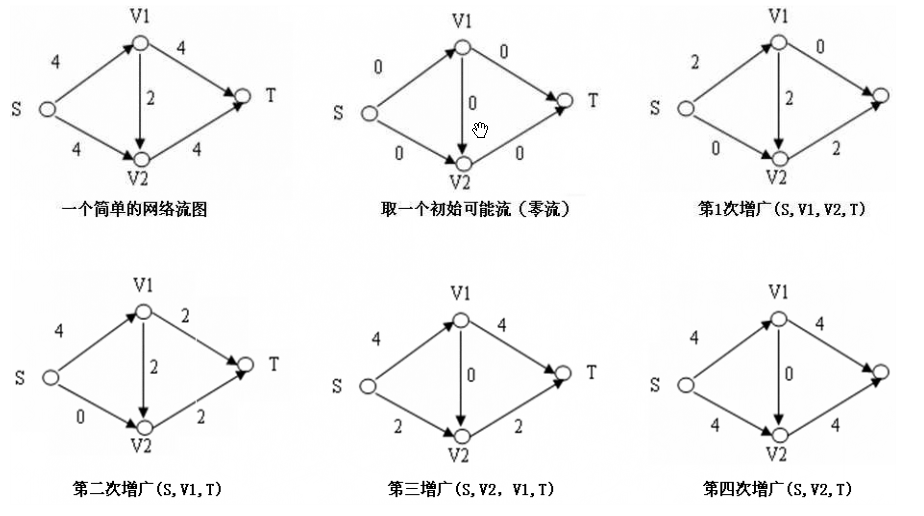
Dinic
BFS 分层
与EK一样,我们仍要通过 bfs 来判断图中是否还存在增广路,但是 Dinic 算法里的 bfs 略有不同。这次,我们不用记录路径,而是给每一个点分层,对于任意点 i,从 s 到 i 每多走过一个点,就让层数多 1。一次分层后可以找到多条增广路,从而提高效率。
分完层效果是这样的:(蓝色的数字是每个点层数)
DFS 增广
有了每个点的层数编号,对任意点 u 到点 d 的路径如果有 $dep[d]=dep[u]+1$,我们就可以判断该路径在增广路上。
比如说,我们首先找 s->1->4->t:
第二次,s->1->5->t:
第三次,s->1->3->t:
还有第四条,s->2->3->t:
PS:Dinic 在跑二分图匹配时比匈牙利快很多。
P3376 网络最大流
1 |
|
