浅谈 Splay（一）

1. 右旋（Right Rotation）

观察每个节点的变化，其中每个节点都有指向其父节点的指针没有画出。

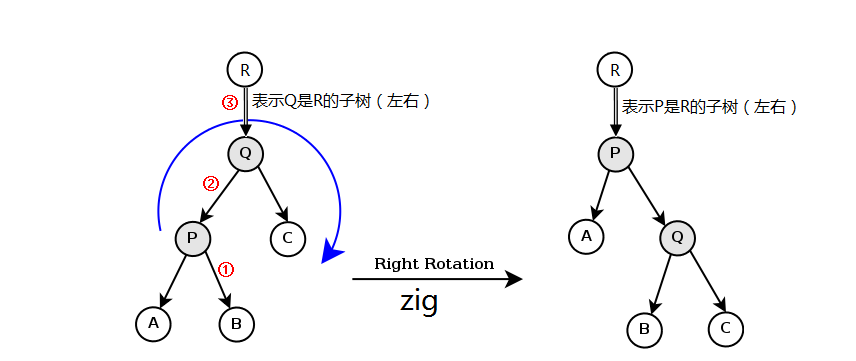
①②③处节点连接有变化。

（1）$Q$ 的左子树修改为 $P$ 的右子树的内容

即 $B$ 成为 $Q$ 的左子树， $B$ 的父节点是 $Q$ 。

q->left = p->right; 
p->right->father = q; 

注意 P​ 可能没有右子树（即不存在 P->right 节点）。

修改如下：

q->left = p->right; 
if(p->right != NULL) p->right->father = q;

（2）$P$ 的右子树修改为 $Q$ ，且同时 $Q$ 的父节点修改为 $P$ 。

p->right = q; 
q->father = p;

注意 Q 和 P 的左右子树有变化，所以 Q,P 的信息需要重新维护。

update(q); update(p); //先Q后P

（3）$R$ 的子树应该修改为 $P$

需要判断 $Q$ 是 $R$ 的哪种子树，左子树则 $P$ 给 $R$ 的左子树，否则给右子树。

全局变量 $root$ 记录树根。

特判 $Q$ 有可能就是树根（即 $R$ 不存在）；

if(r == NULL) {
   p->father = NULL; root = p; return;
}
if(q == r->left) {
   r->left = p; p->father = r;
} else {
   r->right = p; p->father = r;
}

整理一下，不管 Q​ 有无父节点，P 的父节点均修改为 Q 的父节点。

p->father = r;
//记录树根
if(r == NULL) { root = p; return; }
//判断P连到R的那颗子树
if(q == r->left) r->left = p; 
else r->right = p; 

Code :

void right_rotate(node *p) {

    node *q = p->father;     //记录p的父节点
    node *r = q->father;     //记录p的父节点的父节点

    //操作1
    q->left = p->right; 
    if(p->right != NULL) p->right->father = q;

    //操作2
    p->right = q; q->father = p;

    //维护节点信息（注意此处可暂不维护P）
    update(q); //update(p);

    //操作3
    p->father = r;
    if(r == NULL) { root = p; return; }
    
    if(q == r->left) r->left = p; 
    else r->right = p;
}

2、左旋（Left Rotation）

同理右旋，只是①②不同。

Code :

void left_rotate(node *p) {

    node *q = p->father;     //记录p的父节点
    node *r = q->father;     //记录p的父节点的父节点

    //操作1
    q->right = p->left; 
    if(p->left != NULL) p->left->father = q; 

    //操作2
    p->left = q; q->father = p;

    //维护节点信息
    update(q); //update(p);

    //操作3
    p->father = r;
    if(r == NULL){ root = p; return; }
    
    if(q == r->left) r->left = p; 
    else r->right = p;
}

3、双旋

不断旋转 $X$ 节点，为了保证复杂度，需要连续旋转两次且旋转的次序不同。

定义 $X$ 的父节点为 $Y$，$Y$ 的父节点为 $Z$。

（1）$X$ 和 $Y$ 同时是其父节点的左子树或者同时是各自父节点的右子树（即同侧）。

这时我们要进行两次旋转，先旋转 $Y$，再旋转 $X$。

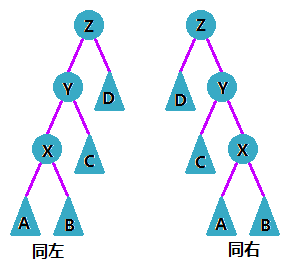
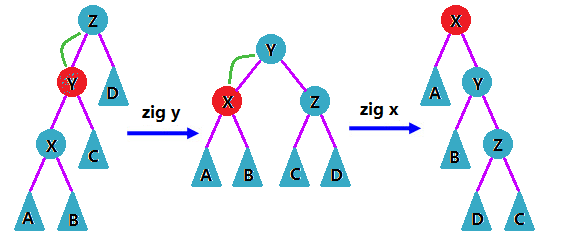
同左旋转演示图如下：

同右旋转演示图如下：

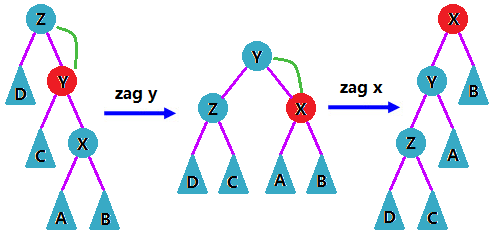
（2）$X$ 和 $Y$ 是其父节点的左、右子树，不同侧（即一左一右或一右一左）。

这时我们只要 旋转两次 X​ 即可。

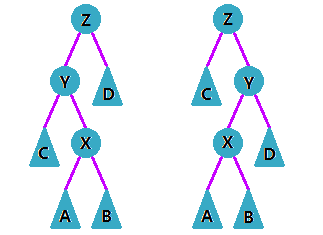
（3）判断 $X$ 节点如何旋转。

$X$ 是其父节点的左子树则右旋，否则左旋。

$X$ 若是它父节点左子树返回 true，否则返回 false：

bool getlr(node *p) {
    return (p->father->left == p);
}
  
//选择合适的旋转方式
void rotate(node *p) {
    if(getlr(p)) right_rotate(p); 
    else left_rotate(p);
}

4、旋转到根

将 $X$ 旋转到根是 splay 的关键，为了保证复杂度，只要对 $X$ 节点操作，操作后就要将其旋转到根。

如何旋转到根：

• 一步旋转就可以到根，进行单旋；

• 两步或两步以上，可以不断使用双旋。

设计函数 splay(p,q) 将 $P$ 旋转到 $Q$ 下方。

• q == NULL 表示 $P$ 旋转到了根；
• while $P$ 至少两次旋转才能到达：双旋；
• if $P$ 还差一步满足条件：单旋。

Code :

void splay(node *p, node *tar) {

      while(p->father != tar and p->father->father != tar) {
          if(getlr(p) == getlr(p->father)) {
              rotate(p->father); rotate(p);
          } else {
              rotate(p); rotate(p);
          }
      }

      if(p->father != tar) rotate(p);
      
      update(p);  //优化（避免重复维护）
}