图论
发表算法13 分钟读完 (大约2024个字)

图论

图论算法一般都是揉在一起的，很难单独把算法拆开讲，所以直接上题目吧。分类是大致分的，其实有很多是交叉的。

二叉树

二叉树的遍历有三种，分别为前序遍历，中序遍历和后序遍历，并且给定其中的两种遍历能够求出另一种遍历 (必须已知中序遍历)。

前序遍历：按 根 左 右 的顺序进行；

中序遍历：按 左 根 右 的顺序进行；

后序遍历：按 左 右 根 的顺序进行。

最短路 & 生成树

算法复杂度

  • 多源最短路Floyd：严格 $O(n^3)$
  • 单源最短路Dijkstra：
    • 朴素：严格 $O(n^2)$
    • 优先队列优化：均摊 $O((e+n) \log n)$
  • Bellman-Ford：
    • 最多松弛 $n-1$ 次
    • 严格 $O(ne)$
  • SPFA：
    • 即队列优化Bellman-Ford
    • 最坏 $O(ne)$，最好 $O(1)$

板子

咕咕咕

如何卡掉 SPFA

见 https://www.zhihu.com/question/292283275/answer/484871888

P1967 货车运输

最大生成树，然后跑LCA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4+10, M = 1e5+10, INF = 0x3f3f3f3f;

struct node {
    int id, u, v, w, next;
} e[M], e1[M];
int h[N], tot = 0, tot1 = 0, n, m;

int fa[N][15], dep[N], dis[N][15];
int vis[N];
bool edg[M];

void add(int u, int v, int w) {
    e1[tot1] = e[tot] = {tot, u, v, w, h[u]}; h[u] = tot++; tot1++;
    e[tot] = {tot, v, u, w, h[v]}; h[v] = tot++;
}

int bc[N];
int root(int u) {
    return bc[u] == u ? u : bc[u] = root(bc[u]);
}

bool cmp(node a, node b) {
    return a.w > b.w;
}
void dfs(int u, int f, int vi) {
    vis[u] = vi;
    for(int i = h[u]; i != -1; i = e[i].next) {
        int v = e[i].v;
        if(v == f) continue;
        if(edg[i] or edg[i^1]) {
            dep[v] = dep[u] + 1;
            fa[v][0] = u;
            dis[v][0] = e[i].w;
            dfs(v, u, vi);
        }
    }
}

void lca(int x, int y) {
    if(dep[x] < dep[y]) swap(x, y);
    int ans = INF;
    int t = dep[x] - dep[y];
    for(int i=14; i>=0; --i) {
        if(t >= (1<<i)) {
            ans = min(ans, dis[x][i]);
            x = fa[x][i];
            t -= (1<<i);
        }
    }
    if(x == y) {
        printf("%d\n", ans);
        return;
    }
    for(int i=14; i>=0; --i) {
        if(fa[x][i] != fa[y][i]) {
            ans = min(ans, dis[x][i]);
            ans = min(ans, dis[y][i]);
            x = fa[x][i]; y = fa[y][i];
        }
    }
    //printf("lca:%d\n", fa[x][0]);
    printf("%d\n", min(ans, min(dis[x][0], dis[y][0])));
}
int main() {
    
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for(int i=1; i<=m; ++i) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w);
    }
    
    sort(e1, e1+tot1, cmp);
    for(int i=1; i<=n; ++i) bc[i] = i;
    for(int i=0; i<tot1; ++i) {
        int u = e1[i].u, v = e1[i].v;
        int u1 = root(u), v1 = root(v);
        if(u1 != v1) {
            edg[e1[i].id] = true;
            bc[v1] = u1;
        }
    }
    
    for(int i=1; i<=n; ++i) {
        if(bc[i] == i) {
            dfs(i, 0, i);
            for(int j=0; j<=14; ++j) {
                fa[i][j] = i;
                dis[i][j] = INF;
            }
        }
    }
    
    for(int i=1; i<=14; ++i) {
        for(int j=1; j<=n; ++j) {
            fa[j][i] = fa[fa[j][i-1]][i-1];
            dis[j][i] = min(dis[j][i-1], dis[fa[j][i-1]][i-1]);
        }
    }
    
    int query; scanf("%d", &query);
    for(int i=1; i<=query; ++i) { 
        int x, y; scanf("%d%d", &x, &y);
        if(vis[x] != vis[y]) { printf("-1\n"); continue; }
        lca(x, y);
    }
    
    return 0;
}

P1073 最优贸易

分层图，最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <stdio.h>
#include <string.h>
#include <limits.h>
#include <iostream>
#include <queue>
#include <map>
using namespace std;

const int N = 330000, M = 1650000;
struct node {
    int u, v, w, next;
    node() {}
    node(int _u, int _v, int _w, int _next): u(_u), v(_v), w(_w), next(_next) {}
} e[M << 1];
int h[N], tot = 0;

inline void add(int u, int v, int w = 0) {
    e[tot] = node(u, v, w, h[u]);
    h[u] = tot++;
}

int n, m, w[N]; bool vis[N]; int dis[N];
int main() {
    
    #ifdef DEBUG
    freopen("p1073_1.in", "r", stdin);
    #endif

    scanf("%d%d", &n, &m);
    for(int i=1; i<=n; ++i) {
        scanf("%d", &w[i]);
    }
    memset(h, -1, sizeof h);
    for(int i=1, x, y, z; i<=m; ++i) {
        scanf("%d%d%d", &x, &y, &z);
        if(z == 1) add(x, y), add(x+n, y+n), add(x+2*n, y+2*n);
        else {
            add(x, y), add(x+n, y+n), add(x+2*n, y+2*n);
            swap(x, y);
            add(x, y), add(x+n, y+n), add(x+2*n, y+2*n);
        }
    }
    
    for(int i=1; i<=n; ++i) {
        add(i+n, i, w[i]);
        add(i, i+2*n, -w[i]);
    }
    
    queue<int> q;
    
    memset(dis, 0x3f, sizeof dis);
    q.push(n+1); vis[n+1] = true; dis[n+1] = 0;
    while(!q.empty()) {
        int u = q.front();
        q.pop(); vis[u] = false;
        for(int i=h[u]; i!=-1; i=e[i].next) {
            int v=e[i].v;
            if(dis[v] > dis[u] + e[i].w) {
                dis[v] = dis[u] + e[i].w;
                if(!vis[v]) {
                    q.push(v);
                    vis[v] = true;
                }
            }
        } 
    }
    
    printf("%d\n", -dis[n*3]);
    
    return 0;
}

P1119 灾后重建

很重要的题目，考察了 Floyd的本质。

Floyd

用 $dis[k][i][j]$ 表示 i 和 j 之间可以通过编号为 $1\dots k$ 的节点的最短路径，显然，$dis[0][i][j]$ 就是原始邻接矩阵数据。

状态转移方程：

$$
dis[k][i][j]=min(dis[k-1][i][j],dis[k-1][i][k]+dis[k-1][k][j])
$$

Floyd 的本质其实就是DP，只不过我们通常做题时利用了数据只会使用一次性的原理，把 dis 变成滚动数组，减少了一维，节省空间。

更多请见 https://www.cnblogs.com/fangwencai/p/4784914.html。

1
2
3
4
5
6
7
//提前将邻接矩阵存在 dis 数组里，其他不连通的地方初始化成无穷大
for(int k=1; k<=n; ++k) //枚举中间点
    for(int i=1; i<=n; ++i) //枚举起点
        if(i != k) //节省时间，如果一样就不往下走
            for(int j=1; j<=n; ++j) //枚举终点
                if(i != j and j != k) //继续判断，如果有一样的就不往下走
                    dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]); //状态转移方程，也就是所谓的松弛操作

只要我们能够利用 DP 特性，就能解决许多问题

再回来看这道题，文中说每个村子是不同时间修好的，而每个节点都按顺序给出，这不就是恰好相当于 Floyd的中间点吗？我们可以把 k轮 DP分开做，每输入一个点，就用这个点当中转站把最短距离更新一遍，也就是跑一遍 DP。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 220;

int t[N];

struct query {
    int id, x, y, t;
} a[55000];

int res[55000], n, m, dp[N][N];
int main() {
    
    //freopen("P1119_2.in", "r", stdin); 
    
    scanf("%d%d", &n, &m);
    
    for(int i=1; i<=n; ++i) {
        scanf("%d", t+i);
    }
    t[n+1] = 0x3f3f3f3f;
    
    memset(dp, 0x3f, sizeof dp);
    
    for(int i=1; i<=n; ++i) dp[i][i] = 0;
    for(int i=1; i<=m; ++i) { int u, v, w;
        scanf("%d%d%d", &u, &v, &w); ++u, ++v;
        dp[u][v] = dp[v][u] = w;
    }
    int q;
    scanf("%d", &q);
    for(int i=1; i<=q; ++i) {
        scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].t);
        a[i].id = i; ++a[i].x, ++a[i].y; 
    }
    
    int cnt = 1;
    for(; a[cnt].t < t[1]; ++cnt) {
        res[a[cnt].id] = -1; 
    }
    
    for(int T=1; T<=n; ++T) {
        
        for(int i=1; i<=n; ++i) {
            for(int j=1; j<=n; ++j) {
                dp[i][j] = min(dp[i][j], dp[i][T] + dp[T][j]);
            }
        }
            
        while(1) {
            if(cnt > q) break;
            if(a[cnt].t >= t[T] and a[cnt].t < t[T+1]); else break;
            if(a[cnt].x > T or a[cnt].y > T or dp[a[cnt].x][a[cnt].y] == 0x3f3f3f3f) {
                res[a[cnt].id] = -1;
            } else {
                res[a[cnt].id] = dp[a[cnt].x][a[cnt].y];
            }
            ++cnt;
        }
    }
    
    for(int i=1; i<=q; ++i) printf("%d\n", res[i]);
    return 0;
}

判负环

转自 @SingerCoder，%lgh

注意一定要判入队次数而不是松弛次数。

hack原理很简单：如果存在重边导致了多次松弛，那么对松弛次数的判断就会产生影响。解决方式就是判入队次数，虽然略慢，但是更稳。

Update[2020.7.26]：在写差分约束的时候想用spfa判无解，然后经过一系列的思考就有了下面这组新的hack数据：

1
2
3
4
5
6
7
8
9
10
11
input:
1
4 6
1 2 -3
1 3 -2
1 4 -1
2 3 -6
2 4 -5
3 4 -4
output:
NO

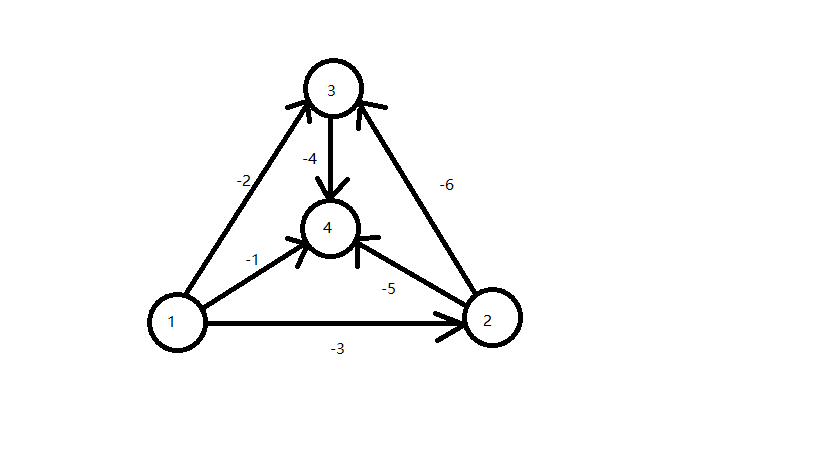
注意这组hack只对用链式前向星（而非vector）存边且判的是松弛次数（而非入队次数）的有效，而且该数据无重边无自环，比discuss里面的那个数据更有说服力。

首先hack原理就是对n号节点进行n-1轮松弛，每轮都有 $x( x \in [1,n-1])$ 次松弛，这样就能产生 $n^2$ 级别的松弛次数。

但是判入队次数就hack不掉了，每轮的第一次松弛会让n节点入队，但n节点只有在下一轮才会出队；因此本轮的其余所有松弛全部无法导致入队。

P3385 [模板]负环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <queue>
using namespace std;

const int N = 2e3 + 10, M = 6e3 + 10;
struct node {
    int u, v, w, next;
} e[M];
int h[N], tot = 0;
int T, n, m;
inline void add(int u, int v, int w) {
    e[++tot] = {u, v, w, h[u]}; h[u] = tot;
} 

int dis[N], vis[N];
bool inq[N];

inline void spfa() {
    
    queue<int> q;
    memset(dis, 0x3f, sizeof dis);
    memset(vis, 0, sizeof vis);
    memset(inq, false, sizeof inq);
    
    dis[1] = 0; q.push(1); inq[1] = true; ++vis[1];
    while(!q.empty()) {
        
        int u = q.front(); q.pop(); inq[u] = false;//printf("%d\n", u);
        for(int i = h[u]; i ; i = e[i].next) {
            int v = e[i].v;
            if(dis[v] > dis[u] + e[i].w) {
                dis[v] = dis[u] + e[i].w;
                if(!inq[v]) {
                    inq[v] = true;
                    ++vis[v];
                    if(vis[v] > n-1) {
                        printf("YES\n");
                        return;
                    }
                    q.push(v);
                }
            }
        }
    }
    printf("NO\n");
}
int main() {
    
    //freopen("P3385_2.in", "r", stdin);
    
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        memset(h, 0, sizeof h); tot = 0;
        for(int i=1; i<=m; ++i) {
            int u, v, w; scanf("%d%d%d", &u, &v, &w);
            if(w >= 0) {
                add(u, v, w);
                add(v, u, w);
            } else add(u, v, w);
            //printf("%d ", i);
        }
        spfa();
    }
    return 0;
}

基环树

n 个点 n 条边 只有一个环 枚举断边

P5022 [NOIp2018TG]旅行

图论

https://snow.js.org/graph-theory/

发布于

2020-07-31

更新于

2023-01-11

许可协议

#

评论

分类

最新文章

标签

AI2
Aplayer1
Butterfly1
DAG1
DFS3
GitHub1
Hexo2
LCA1
PB_DS1
SSH1
STL2
二分图2
动态规划3
匹配2
单调队列2
博客2
双指针1
图书馆4
图论4
小说7
尺取法1
平衡树1
排序2
数学1
数据结构1
数论3
最小割1
最短路4
树1
游记1
码风1
算法25
网络流5
记忆化搜索4
部署1
随感2
随笔1
×